
기하 알고리즘 문제이다. 처음에는 선분의 양 끝 점을 알고 있으므로, 두 개의 1차함수로 만들어 교점을 구해 그 점이 선분위에 있는지 찾는 방법을 사용했다. 두 함수의 기울기가 같을 때만 따로 처리해주었고, 문제에 있는 예제와 다양한 반례들을 넣어봐도 모두 바른 답이 나왔으나 정작 코드를 제출하면 3%에서 틀렸습니다가 발생했다.
아무래도 x의 증분 및 y의 증분을 계산할 때 실수 자료형을 사용해야 하고, 부동 소수점 오차 때문에 문제가 생기는 것 같았다. 그래서 double형을 사용하지 않고, 분수 꼴의 자료형을 커스텀해볼까 하다가 연산 도중에 그럼에도 분모 혹은 분자가 long long의 범위를 넘어갈 수 있어 패스했다. 그 다음엔 오차 범위 이내의 차를 보이면 같은 것으로 취급해 부동 소수점 오차를 보정할까 했으나, 그러기엔 정수부의 길이에 따라 보장할 수 있는 오차 범위가 달라지는 문제가 있었다. 물론, 이를 계산해서 상대적인 오차범위를 설정할 수도 있겠으나, 아름다운 해결책은 아닌 것 같았다.
그러던 와중에, 알고리즘 수업 때 배운 기하 알고리즘이 어렴풋이 떠올랐다. 그 때 CCW 판정을 응용해서 해결할 수 있는 볼록 껍질과 같은 다양한 문제들을 경험했었는데, 두 선분의 교차 여부 확인은 그 중 하나였다.
CCW 판정, 즉 CounterClockWise 판정은 2차원 평면 상에 놓여있는 세 점이 이루는 형태가 반시계 방향인지 확인하는 것이다. 물론 이 방향이라는 것은, 어느 순서로 점을 택하냐에 따라 달라지기 때문에 이에 유의해서 사용해야 한다.
원리는 벡터의 외적을 사용하는 것인데, 점 하나를 기준으로 잡아 벡터 두 개를 만들고, 그 외적 값을 계산한다(z값은 0). 벡터를 곱할 때 먼저 오는 벡터를 기준으로 해서 다른 벡터가 반시계 방향에 놓여있다면 외적은 양수가 되고, 시계 방향에 놓여 있다면 외적은 음수가 된다. 그리고 외적 값이 0이라면 두 벡터가 평행한 경우이다.
따라서, CCW 알고리즘의 결과가 양수라면 세 점은 반시계 방향, 음수라면 시계 방향에 놓인 것이고, 0이라면 한 직선 위에 놓인 것이다. 이 CCW 알고리즘을 통해 두 선분의 교차 여부를 판별한다.
먼저 두 선분 A와 B에 각각 양 끝 점을 a1, a2, b1, b2라고 한다. 두 선분이 교차하는 경우를 생각해보면, 어떻게 놓이든 간에 CCW(a1, a2, b1)와 CCW(a1, a2, b1)의 부호가 다르고, CCW(b1, b2, a1)와 CCW(b1, b2, a2)의 부호가 다르다는 것을 알 수 있다. 하지만 이것만 이용해서는 한 선분에 다른 선분의 끝점이 접하는 경우는 판별할 수 없다.
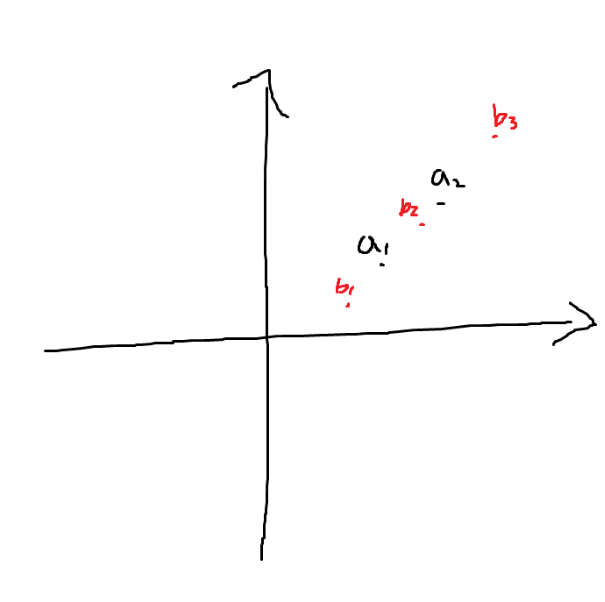
이 경우는 따로 처리해주어야 하는데, 만약 저 네 경우의 CCW를 구하는 도중 CCW(a1, a2, b)의 결과로 0이 나왔다고 할 때, 위 그림을 기준으로 점 b가 b1, b2, b3에 놓여있을 수 있는 것이다. 따라서 이 때는 점 b가 점 a1과 a2를 잇는 선분 위에 놓여 있는지를 판별해주면 된다(a1=b 이거나 a2=b 인 경우도 선분 위에 놓인 경우다). 그 점이 선분 위에 놓여 있다면, 이는 어떠한 형태로든 해당 끝점이 선분에 접하는 경우이므로, 이 때도 교차하는 경우로 판별한다.
교차하지도, 접하지도 않는 경우는 당연히 두 선분이 교차하지 않는 경우로 판별한다.
교수님께서 학기 막바지에 알려주셨던, 유전학 알고리즘이나 문자열 관련 알고리즘, 기하 알고리즘 등이 막상 배울 때는 전공책에도 없고 조금 어렵게 느껴졌었는데, 지나고 보니 응용할 곳도 많고 도움이 많이 되는 것 같다..
#include <iostream>
using namespace std;
typedef pair<int, int> point;
typedef pair<int, int> vector;
vector getVector(point start, point end) {
return {end.first - start.first, end.second - start.second};
}
int getCCW(vector start, vector end) {
long long crossProduct = (long long)start.first*end.second - (long long)start.second*end.first;
if(crossProduct > 0) {
return 1;
} else if(crossProduct == 0) {
return 0;
} else {
return -1;
};
}
bool isOnLine(point a1, point a2, point b) {
int aMinX, aMaxX, aMinY, aMaxY;
if(a1.first<a2.first) {
aMinX = a1.first;
aMaxX = a2.first;
} else {
aMinX = a2.first;
aMaxX = a1.first;
}
if(a1.second<a2.second) {
aMinY = a1.second;
aMaxY = a2.second;
} else {
aMinY = a2.second;
aMaxY = a1.second;
}
return aMinX<=b.first && aMaxX>=b.first && aMinY<=b.second && aMaxY>=b.second;
}
int main() {
point a1, a2, b1, b2;
cin >> a1.first >> a1.second >> a2.first >> a2.second >> b1.first >> b1.second >> b2.first >> b2.second;
int aToB1, aToB2, bToA1, bToA2;
aToB1 = getCCW(getVector(a1, a2), getVector(a2, b1));
aToB2 = getCCW(getVector(a1, a2), getVector(a2, b2));
bToA1 = getCCW(getVector(b1, b2), getVector(b2, a1));
bToA2 = getCCW(getVector(b1, b2), getVector(b2, a2));
if(aToB1==0 && isOnLine(a1, a2, b1) ||
aToB2==0 && isOnLine(a1, a2, b2) ||
bToA1==0 && isOnLine(b1, b2, a1) ||
bToA2==0 && isOnLine(b1, b2, a2)) {
cout << "1";
} else if (aToB1*aToB2==-1 && bToA1*bToA2==-1) {
cout << "1";
} else {
cout << "0";
}
}'Dev > BOJ' 카테고리의 다른 글
| [백준 1647] 도시 분할 계획 (0) | 2024.08.29 |
|---|---|
| [백준 1644] 소수의 연속합 (6) | 2024.08.28 |
| [백준 14003] 가장 긴 증가하는 부분 수열 5 (0) | 2024.08.26 |
| [백준 13460] 구슬 탈출 2 (0) | 2024.08.25 |
| [백준 12015] 가장 긴 증가하는 부분 수열 2 (0) | 2024.08.24 |



