
수학 기반 구현 문제다. 구간 사이의 모든 이진수 형태의 자연수에 대해 하나하나 1의 개수를 구하면 시간 내에 풀 수 없다. DP를 활용한다고 해도 A가 1이고 B가 10^16를 생각해 보면 시간초과가 발생함을 알 수 있다.
이런 이진수 꼴을 활용하는 문제가 으레 그러하듯이, 최상위 비트가 1이고 나머지가 0으로 채워진 경우나 모든 비트가 1로 채워진 경우를 나열해서 관계식을 찾아내는 것이 중요하다.
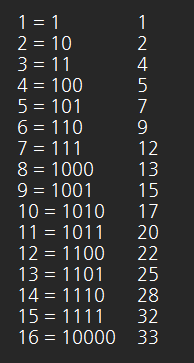
나는 연속된 자연수에 대한 각각의 1의 개수와 이전까지 등장했던 1의 개수 합 등을 써보며 관계식을 찾으려 했다. 위처럼 1의 개수 누적합을 나열했을 때, 유의미한 관계식을 찾아냈는데 (2^n)-1의 등장 1 개수 누적합은 (2^(n-1))-1일 때 값의 2배에 2^(n-1)를 더한 값이다. 이렇게 글로 써두면 복잡해 보이지만 식을 직접 나열해 보면 쉽게 보인다.

이 f(x)=f((2^n)-1) (n은 0 이상의 정수)에서, x=1(2), 11(2), 111(2), 1111(2), ... 일 때 성립하며, 이는 2^n번째 비트가 1이고 나머지 비트가 0인 자연수가 등장하기 직전까지 누적되어 온 1의 합을 의미한다.
이걸 이용한다면 O(log n)의 복잡도로 특정 자연수를 이진수로 나타냈을 때 1 개수를 구할 수 있다. 여기부턴 취향껏 구현하면 되는데, 나는 최상위 1비트를 찾아서 한 자리씩 오른쪽으로 옮겨 가며 계산하는 방법으로 구현했다.
만약 10010(2)라면, 2^4 자리에 해당하는 비트부터 시작한다. 비트를 하나하나 탐색하며 등장하는 1의 수를 저장하는 변수 appearanceOne과 결과로 리턴할 자연수 n까지의 1 개수 합을 저장하는 변수 totalOneNum을 둔다. 그리고 아까 찾아둔 비트부터 루프를 시작하는데 먼저 해당 자리의 비트가 1인지 확인한다. 만약 1이라면 그 1이 등장하기 이전까지 등장한 수들에 대해 고려해줘야 한다. 10000(2)이 있으려면 그 이전에 0(2), 1(2), 10(2), 11(2), ... ,1111(2)이 있었을 테니까.
따라서 탐색 중인 비트가 1이라면 미리 구해둔 위의 1 개수 배열에서 이전까지 등장했을 1 개수 합을 찾아 totalOneNum에 더한다. 2^4자리를 탐색 중이었다면 1111(2)까지의 1 개수 합을 더해주는 것이다.
그리고 appearanceOne * 2^(탐색 중인 비트 위치-1) 값을 totalOneNum에 추가적으로 더해준다. 만약 10010(2)에 대해 가장 왼쪽의 1에 대해 계산을 해주고, 2^1 위치의 비트에 도달했다고 생각해 보자. 그러면 현재까지 더해진 것은 0(2)부터 1111(2)까지다. 이 위치의 비트를 이용해서 구하게 되는 것은 0(2)부터 1(2)의 합이 되는 것인데, 사실 실제로 필요한 것은 10000(2)부터 10001(2)에 해당하는 부분이다. 앞서 등장한 1비트 수(appearanceOne) * 이번 연산으로 더해지는 원소 수(2^(탐색 중인 비트 위치-1))만큼을 더해줘야, 0(2)부터 1(2)을 고려하는 것이 아닌 10000(2)부터 10001(2)을 고려하게 되는 것이다.
물론 탐색 중인 비트가 0이라면 따로 추가해주지 않고 넘어가게 되며, 비트 판정을 마친 후엔 탐색 중인 비트 자리를 오른쪽으로 한 칸 옮겨주면 된다.
이렇게 모든 루프를 끝내면(모든 비트를 탐색 완료), 10010(2)을 구하려 했다면 0(2)부터 10001(2)까지의 1 개수가 구해진 상태이다. 마지막 10010(2)의 1 개수를 더해줘야 하는데, 이는 appearanceOne에 저장돼 있으므로 이를 더해 리턴한다.
이제 [A, B] 구간에 대해 1 개수 합을 구하려면 단순하게 누적합이니까 B에 대한 위 함수 결과에서 A-1에 대한 위 함수 결과를 빼주면 된다. 개인적으로 이 과정들 속에서 굳이 나누기나 모듈러 연산을 활용하기보단, 비트 연산을 활용하면 속도도 빠르고 더 직관적으로 작성할 수 있어 좋다고 생각한다.
뭔가 설명하기가 더 어려웠던 문제 같다..
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
vector<ll> oneList;
void fillOneList(ll num) {
ll ex = 1;
ll curSum = 0;
while(ex<=num) {
oneList.push_back(curSum);
curSum = (curSum << 1) + ex;
ex = ex << 1;
}
}
ll getOneNum(ll num) {
ll totalOneNum = 0;
ll appearanceOne = 0;
int bitInd = 0;
ll twoMutiple = 1;
while(twoMutiple <= num) {
bitInd++;
twoMutiple = twoMutiple<<1;
}
ll bitCursor = 1LL << bitInd-1;
bitInd--;
while(bitCursor>0) {
if(num & bitCursor) {
totalOneNum += oneList[bitInd];
totalOneNum += appearanceOne * 1<<bitInd;
appearanceOne++;
}
bitCursor = bitCursor >> 1;
bitInd--;
}
totalOneNum += appearanceOne;
return totalOneNum;
}
ll getOneNumInRange(ll start, ll end) {
fillOneList(end);
return getOneNum(end)-getOneNum(start-1);
}
int main() {
ll a, b;
cin >> a >> b;
cout << getOneNumInRange(a, b);
}
'Dev > BOJ' 카테고리의 다른 글
| [백준 11401] 이항 계수 3 (2) | 2024.09.07 |
|---|---|
| [백준 10775] 공항 (4) | 2024.09.06 |
| [백준 2568] 전깃줄 - 2 (1) | 2024.09.04 |
| [백준 2342] Dance Dance Revolution (1) | 2024.09.03 |
| [백준 2162] 선분 그룹 (0) | 2024.09.02 |



