
그래프 탐색 문제로, 내가 좋아하는 문제 시리즈 중 하나다. 가장 먼저 직관적으로 떠올릴 수 있는 알고리즘은 모든 벽이 있는 칸에서 DFS나 BFS를 돌리는 것이겠지만, 조금만 생각해 봐도 시간 초과가 날 수 있음을 예상할 수 있다. N과 M이 모두 1,000이고, 0번째 행과 999번째 행이 모두 벽, 나머지 공간에는 벽이 없는 경우를 생각해 보면 된다. 혹시나 시간이 초과될만한 예시를 당장 떠올리지 못했더라도, 시간 복잡도가 명확하게 가늠되지 않는 알고리즘은 사용하지 않는 것이 좋다.
해결 방법은 심플한데, 맵을 먼저 탐색하며 빈칸 집합끼리 나눠주고 그 영역에 존재하는 빈 공간 수를 저장해 둔다. 그리고 실제 결과를 출력하기 위한 탐색을 용이하게 만들기 위해서 빈칸이 소속된 영역을 레퍼런싱 할 수 있게 처리를 해두는 것이 좋다.
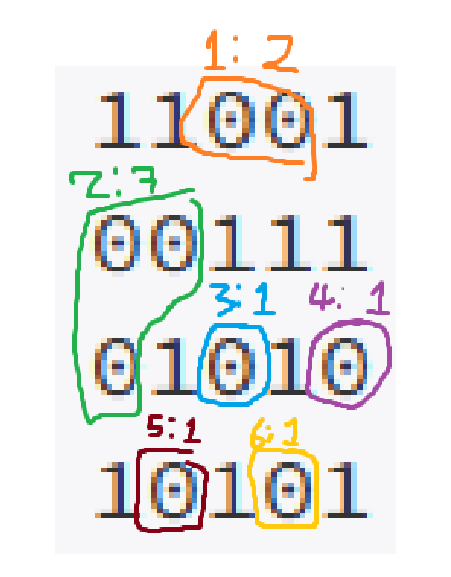
예제 입력 2를 예로 들자면, 저런 식으로 영역이 6군데가 나오게 되며 탐색 과정에서 그 크기도 알 수 있다. 모든 탐색을 끝내서, 영역에 대한 정보를 확보했다면 이제 다시 그래프를 탐색하며 이번엔 벽이 있는 곳들을 찾는다.
그리고 그 벽 위치의 상하좌우를 확인해, 영역이 있다면 그 영역의 넓이를 모두 더하고 벽을 부수는 상황을 상정하므로 본인 위치 1칸을 더해 모듈러 10 연산을 해주면 해당 좌표에서 벽을 부수고 향할 수 있는 모든 칸의 수를 10으로 나눈 나머지가 된다. 이때, 상하좌우의 영역이 같은 영역일 수도 있기 때문에, 중복된 영역은 포함하지 않도록 해야 한다. 중복체크를 할 땐 매번 상하좌우만 확인하므로 탐색하는 원소 수가 항상 4밖에 되지 않아서, 나는 배열을 이용해서 중복체크를 했다.
이렇게 하면 두 번의 그래프 탐색은 각각 O(N * M)의 시간 복잡도를 가지므로, 부가적으로 걸리는 시간을 고려하더라도 넉넉하게 통과할 수 있다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int dx[4] = {1, 0, -1, 0};
int dy[4] = {0, 1, 0, -1};
int matrix[1000][1000];
bool isVisited[1000][1000];
int main() {
cin.tie(nullptr);
ios_base::sync_with_stdio(false);
int n, m;
cin >> n >> m;
string input;
for(int i=0; i<n; i++) {
cin >> input;
for(int j=0; j<m; j++) {
if(input[j]=='0') {
matrix[i][j] = 0;
} else {
matrix[i][j] = -1;
}
}
}
vector<int> areaSet;
areaSet.push_back(0); //dummy
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(matrix[i][j]==0) {
queue<pair<int, int> > q;
q.push({i, j});
areaSet.push_back(0);
int setInd = areaSet.size()-1;
while(!q.empty()) {
auto point = q.front();
q.pop();
if(matrix[point.first][point.second]!=0) continue;
areaSet[setInd]++;
matrix[point.first][point.second] = setInd;
for(int k=0; k<4; k++) {
int newY = point.first+dy[k];
int newX = point.second+dx[k];
if(newY>=0 && newY<n && newX>=0 && newX<m && matrix[newY][newX]==0) {
q.push({newY, newX});
}
}
}
}
}
}
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(matrix[i][j]==-1) {
int sum = 0;
int consumedNumList[4]={0,0,0,0};
for(int k=0; k<4; k++) {
int newY = i+dy[k];
int newX = j+dx[k];
if(newY>=0 && newY<n && newX>=0 && newX<m && matrix[newY][newX]!=-1) {
bool consumedFlag = false;
for(auto consumedNum: consumedNumList) {
if(consumedNum==matrix[newY][newX]) {
consumedFlag = true;
break;
}
}
if(!consumedFlag) {
sum += areaSet[matrix[newY][newX]];
consumedNumList[k] = matrix[newY][newX];
}
}
}
cout << (sum+1)%10;
} else {
cout << "0";
}
}
cout << "\n";
}
}
'Dev > BOJ' 카테고리의 다른 글
| [백준 20040] 사이클 게임 (0) | 2024.09.14 |
|---|---|
| [백준 17404] RGB거리 2 (0) | 2024.09.11 |
| [백준 16724] 피리 부는 사나이 (0) | 2024.09.09 |
| [백준 11401] 이항 계수 3 (2) | 2024.09.07 |
| [백준 10775] 공항 (4) | 2024.09.06 |



