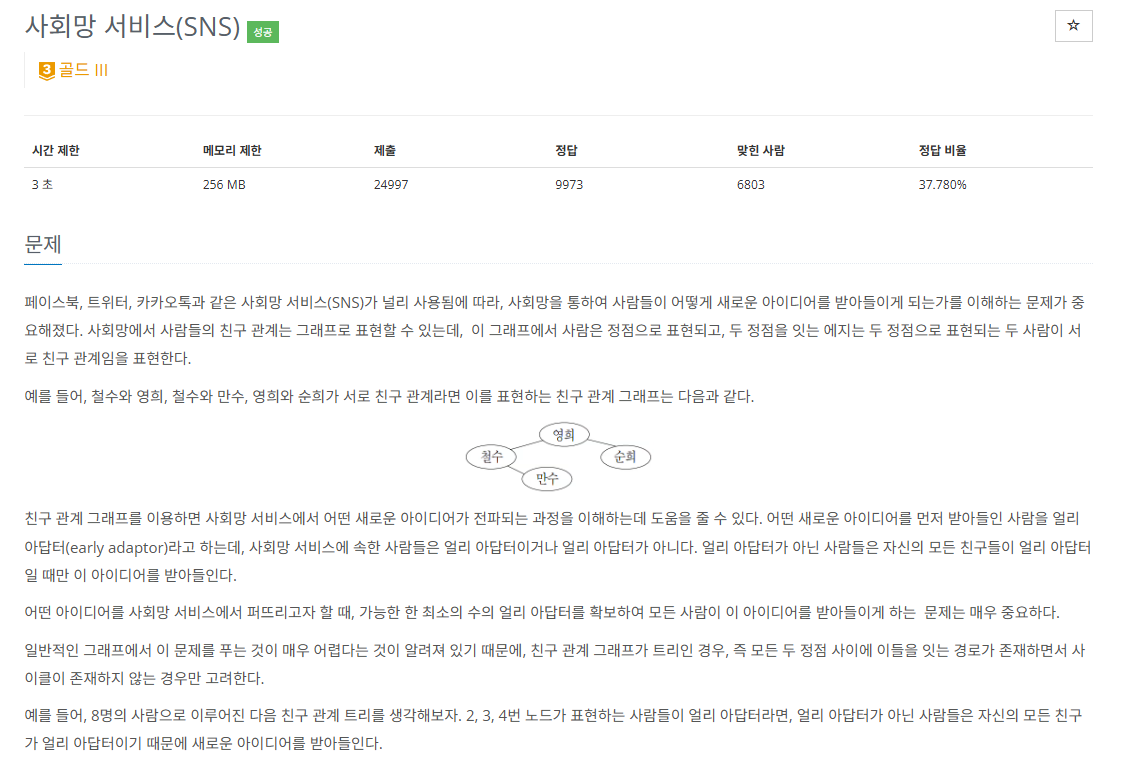

DP 문제다. 처음에는 트리의 레벨을 홀수 레벨과 짝수 레벨로 나누어 해당하는 노드 수를 센 다음에 더 작은 값을 출력하는 그리디 알고리즘으로 풀 수 있지 않을까 생각했는데, 예제2만 봐도 성립하지 않음을 알 수 있었다.
좀 더 고민해봐도 일반적인 그래프 탐색을 이용해서는 풀 수 없을 것 같아서 다른 알고리즘을 생각하다가 DP를 도입해 해결했다.
문제 해결을 위해 각 노드에 대해 고려해 보아야 하는 상태는 해당 노드가 얼리 아답터인 경우와 아닌 경우다. 문제에서 주어지는 그래프가 트리임을 보장하고 있으므로, 어떤 한 노드를 루트 노드로 설정하면 모든 노드에 대해 부모 노드와 자식 노드를 정할 수 있다.
i번 째 노드에 대해, dp[i][0]를 i번 째 노드가 얼리 아답터일 때 서브 트리의 최소 얼리 아답터 수로 두고, dp[i][1]를 i번 째 노드가 얼리 아답터가 아닐 때 서브 트리의 최소 얼리 아답터 수로 둔다.
그 이후에 각 dp값을 구하는 로직을 생각해봐야 하는데, dp[i][1]은 문제 조건에 의해 모든 자식 노드에 대해 dp[자식 인덱스][0] 값을 더한 값임을 알 수 있다. 탐색 중인 노드가 얼리 아답터가 아니려면 자식과 부모가 모두 얼리 아답터여야 할 테니까.
dp[i][0]의 경우에는 조금 다른데, 해당 노드가 얼리 어답터라고 한들 자식 노드가 얼리 아답터가 아닌 경우가 최적해임을 보장할 수 없다. 자식 노드가 하나인데 손자 노드가 수백 개이고 그 손자 노드들이 모두 리프 노드인 경우를 생각해 보면 된다. 따라서 dp[i][0]는 모든 자식 노드에 대해 min(dp[자식 인덱스][0], dp[자식 인덱스][1]) 값을 더해주어야 한다.
그리고 만약 탐색 중인 노드가 리프 노드라면 당연히 dp[i][0]은 1이고, dp[i][1]은 0이 될 것이다. 따라서 종료 조건도 명확하므로 이는 재귀를 통해 탐색할 수 있다.
이제 위의 로직을 종합해서 임의의 루트 노드를 하나 설정하고 재귀적으로 dp 값을 탐색한다음, 해당 루트 노드의 min(dp[][0], dp[][1])을 출력하기만 하면 된다. 발상하는데 어려움이 없다면 구현은 간단했던 문제.
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n;
vector<vector<int> > adjList;
vector<bool> isVisited;
vector<vector<int> > dp; //{{isEarlyAdpt, isNotEarlyAdpt}}
void traversal(int n) {
isVisited[n] = true;
dp[n][0] = 1;
for(int adj: adjList[n]) {
if(!isVisited[adj]) {
traversal(adj);
dp[n][1]+=dp[adj][0];
dp[n][0]+=min(dp[adj][0], dp[adj][1]);
}
}
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
int node1, node2;
adjList = vector<vector<int> >(n+1, vector<int>());
isVisited = vector<bool>(n+1, false);
dp = vector<vector<int> >(n+1, vector<int>(2, 0));
for(int i=0; i<n-1; i++) {
cin >> node1 >> node2;
adjList[node1].push_back(node2);
adjList[node2].push_back(node1);
}
traversal(1);
cout << (dp[1][0]<dp[1][1] ? dp[1][0] : dp[1][1]);
}
'Dev > BOJ' 카테고리의 다른 글
| [백준 11505] 구간 곱 구하기 (0) | 2024.10.14 |
|---|---|
| [백준 11054] 가장 긴 바이토닉 부분 수열 (3) | 2024.10.13 |
| [백준 2042] 구간 합 구하기 (0) | 2024.10.11 |
| [백준 2357] 최솟값과 최댓값 (0) | 2024.10.10 |
| [백준 1019] 책 페이지 (4) | 2024.10.09 |



